Regular Expressions
1 Regular expressions
We will consider the basic version of regular expressions.
Regular expressions are expressions in a language over alphabet \(\Sigma\).
Base case:
If a symbol \(x\in\Sigma\), then \(x\) is a RE with the language \(L(x) = \{x\}\)
Concatenation:
If \(e_1\) and \(e_2\) are RE, then \(e_1 e_2\) is a RE with the language \(L(e_1e_2) = \{st: s\in L(e_1), t\in L(e_2)\}\).
Alternation:
If \(e_1\) and \(e_2\) are RE, then \(e_1 | e_2\) is a RE with the language \(L(e_1|e_2) = L(e_1)\cup L(e_2)\).
Optional:
If \(e\) is RE, then \(e?\) is a RE with \(L(e?) = L(e)\cup\{\epsilon\}\).
Repeatition:
If \(e\) is RE, then \(e*\) is a RE with \(L(e*) = \bigcup_{k=0}^{\infty}\{s_1s_2\dots s_k: s_i\in L(e)\}\)
A language \(L\) is regular if there exists some RE \(e\) such that \(L = L(e)\).
All regular languages are denoted as \(\mathcal{L}(\mathbf{RE})\).
So far, we have presented three ways of defining languages:
- \(\mathcal{L}(\mathbf{NFA})\)
- \(\mathcal{L}(\mathbf{DFA})\)
- \(\mathcal{L}(\mathbf{RE})\)
It turns out that they are all equivalent.
2 Thompson’s Construction
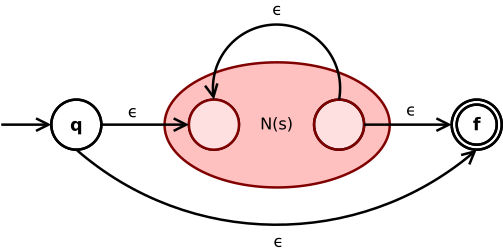
Thompson’s construction is an algorithm that converts a RE to a NFA with the equivalent language.
\(N(a)\)

\(N(s|t)\)

\(N(st)\)
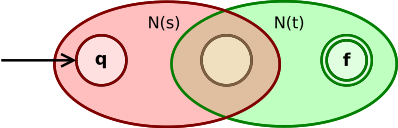
\(N(s*)\)
\[ \mathcal{L}(\mathbf{RE}) = \mathcal{L}(\mathbf{NFA}) = \mathcal{L}(\mathbf{DFA}) \]
3 Limitations of Regular Languages
Consider a family of languages:
\(L_0 = \{\epsilon\}\)
\(L_1 = \{01\} \cup L_0\)
\(L_2 = \{0011\} \cup L_1\)
\(L_3 = \{000111\} \cup L_2\)
\(\vdots\)
\(L_n = \{\underbrace{0\dots 0}_{n}\ \underbrace{1\dots 1}_{n}\} \cup L_{n-1}\)
Claim:
For any specific \(n\), \(L_n\) is regular. Here is the NFA for \(L_3\).
Observe however, as \(n\) increases, \(\mathbf{NFA}(L_n)\) requires more states.
Now, consider the language \(L_\infty\). This is the language containing any string with 0’s followed by 1’s with the same number of 0’s and 1’s.
\[ L_\infty\not\in\mathcal{L}(\mathbf{NFA}) \]
By the theorem, \(L_\infty\) is not RE.
4 RE, NFA, DFA and Anltr
We define lexical rules in Antlr using RE.
Antlr converts all lexical rules into a single combined NFA for efficiency.
Antlr converts the combined NFA into a DFA for memory efficiency.
Lexical analysis in Antlr is done by running the DFA that corresponds to all the user-defined token patterns as regular expressions.