Ambiguous Grammars

Author

Ken Pu

1 Grammar rewrite

We say that two grammars \(G\) and \(G'\) are equivalent if they define the same language.

\[ L(G) = L(G') \]

Even if two grammars \(G\) and \(G'\) have the same language, they may be quite different and have different properties.

2 Ambiguity of grammars

Definition: ambiguous grammars

A grammar \(G\) is ambiguous if there exists at least one sentence \(x\in L(G)\) with two distinct parse trees.

2.1 Some theoretical result

Theorem: Rohit Parikh, 1961

There exists an inherently ambiguous language. Namely, there exists some langauge \(L\subseteq\Sigma^*\) such that every grammar \(G\) that defines \(L\) must be ambiguous:

\[ L(G) = L \implies G \mathrm{\ is\ ambiguous} \]

Theorem: Emil Post, 1946

Recognizing ambiguity of a grammar is undecidable.

2.2 Ambiguity of arithmetics

\[ \begin{eqnarray} E &:& \mathrm{Number}\ |\ E + E\ |\ E * E \end{eqnarray} \]

Given a string \(x = a + b * c\) where \(a, b, c\) are tokens of type \(\mathrm{Number}\). There are two distinct derivations of \(x\), and have the following parse trees:

       E              E
     / | \          / | \
    E  *  E        E  +  E
  / | \   |        |   / | \
 E  +  E  c        a  E  *  E
 |     |              |     |
 a     b              b     c

2.3 Ambiguity of if-then-else

Another example of ambiguous grammar is in the definition of if-then-else in procedural languages.

stmt : if expr then stmt
     | if expr then stmt else stmt
     | other...

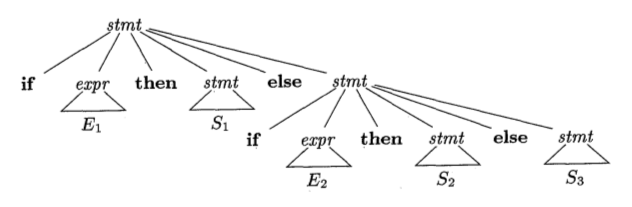
Consider the sentence:

if E1 then S1 else if E2 then S2 else S3

There is only one parse tree:

image.png

But now, consider another sentence:

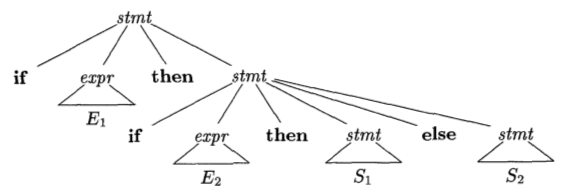
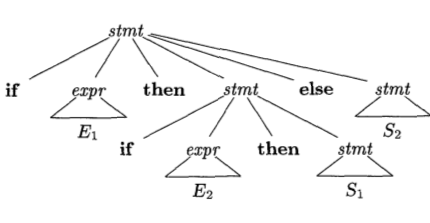
if E1 then if E2 then S1 else S2

This is known as the dangling-else statement.

It has two parse trees:

Tree 1 Tree 2
image.png image.png
Challenge

Can you come up with an instance for E1, E2 such that the two parse trees execute different statements (S1, S2, or none).

3 Elimination of ambiguity using grammar rewriting

The objective is to rewrite a grammar \(G\) to \(G'\) such that:

  • \(L(G) = L(G')\)
  • \(G'\) is not ambiguous.

This is not always possible due to Parikh’s theorem.

Even if it’s possible, it cannot be solved algorithmically due to Post’s theorem.

Revised objective

We want to identify known ambiguous fragments of the grammar, and fix them.

3.1 Fixing ambiguity in arithmetics

3.1.1 Intuition

  • Consider a potentially ambiguous expression:

    1 + 2 * 3 + 4 * 5

  • A factor is either a number or an expression enclosed by parentheses.

  • A term is one or more factors multiplied or divide together. \[ \mathrm{term} : \mathrm{factor} * \mathrm{factor} * \dots \]

  • A expression is one or more terms added (or subtract) together. \[ \mathrm{expression} : \mathrm{term} + \mathrm{term} + \dots \]

3.1.2 The ambiguous arithmetics grammar

\[ \begin{eqnarray} E &:& \mathrm{Number} \\ &|& E\ *\ E \\ &|& E\ /\ E \\ &|& E\ +\ E \\ &|& E\ -\ E \\ &|& (\ E\ ) \end{eqnarray} \]

Let’s fix it by introducing terms and factors.

\[ \begin{eqnarray} E &:& \mathrm{Term} \\ &|& \mathrm{Term} + E \\ &|& \mathrm{Term} - E \\ \mathrm{Term} &:& \mathrm{Factor} \\ &|& \mathrm{Factor} * \mathrm{Term} \\ &|& \mathrm{Factor} / \mathrm{Term} \\ \mathrm{Factor} &:& \mathrm{Number} \\ &|& ( E ) \end{eqnarray} \]

Challenge

  1. Is 1 + 2 * 3 a sentence of the new grammar?

  2. How many distinct parse trees can be constructed for 1 + 2 * 3?

3.2 Fixing ambiguity of dangling-else expressions

3.2.1 Intuition

  • We distinguish two types of if-then statements:

    Matched statements

    It is either a non-if statement, or a complete if-then-else statement.

    Open statements

    It is either a if-then statement (without else), or it is a if-then-else statement but the else-statement is an open statement.

3.2.2 The ambiguous grammar

\[ \begin{eqnarray} \mathrm{stmt} &:& \mathbf{if}\ E\ \mathbf{then}\ \mathrm{stmt} \\ &|& \mathbf{if}\ E\ \mathbf{then}\ \mathrm{stmt}\ \mathbf{else}\ \mathrm{stmt} \\ &|& \mathit{others}\dots \end{eqnarray} \]

3.2.3 The unambiguous grammar

\[ \begin{eqnarray} \mathrm{stmt} &:& \mathrm{matchedStmt} \\ &|& \mathrm{openStmt} \\ \mathrm{matchedStmt} &:& \mathbf{if}\ E\ \mathbf{then}\ \mathrm{matchedStmt}\ \mathbf{else}\ \mathrm{matchedStmt} \\ &|& \mathit{others}\dots \\ \mathrm{openStmt} &:& \mathbf{if}\ E\ \mathbf{then}\ \mathrm{stmt}\\ &|& \mathbf{if}\ E\ \mathbf{then}\ \mathrm{matchedStmt}\ \mathbf{else}\ \mathrm{openStmt} \end{eqnarray} \]

Challenge
  • Is if E1 then if E2 then S1 else S2 a sentence of the revised grammar?
  • Can you construct two distinct parse tree for it?

4 Grammar Design

Rewriting grammar to remove ambiguity cannot be automated. What if we can avoid ambiguity by changing the syntax of the language.

4.1 Redesigning arithmetics

\[ \begin{eqnarray} E &:& F \\ &|& F + F \\ &|& F * F \\ F &:& \mathrm{Number}\ |\ ( E ) \end{eqnarray} \]

  • Is 1 + 2 * 3 part of the language \(L(E)\)?
    No: it needs to be:
    • 1 + (2 * 3), or
    • (1 + 2) * 3
  • Is the new language ambiguous?
    No.
  • Is the new language design a good idea?
    Probably not.

4.2 Redesigning if-then-else

\[ \begin{eqnarray} \mathrm{stmt} &:& \mathbf{if}\ E\ \mathbf{then}\ \{ \mathrm{stmt} \} \\ &|& \mathbf{if}\ E\ \mathbf{then}\ \{ \mathrm{stmt} \}\ \mathbf{else}\ \{ \mathrm{stmt}\} \\ &|& \mathit{others}\dots \end{eqnarray} \]

  • Is if E1 then if E2 then S1 else S2 part of the language \(L(E)\)?
    No: it needs to be:

    if E1 then {
  if E2 then {
    S1
  } else {
    S2
  }
}

  • Is the new language ambiguous?
    No.

  • Is the new language design a good idea?
    Probably yes.

5 Summary

  • Ambiguity leads to unpredictable execution of code.

  • Sometimes, we can eliminate the ambiguity by means of grammar rewrites while preserving the syntax.

  • Sometimes, we can redesign the language so the natural grammar is not ambiguous.